认识二分法
通俗地解释二分法是什么,那我最先想到的是猜数字。玩家通过不断缩小包含目标值的区间范围,直到选择到只剩下一个值,也就是要找到的最终目标值。需要注意的是,仅当列表是有序的时候,二分查找才是管用的。
运行时间
假设我们在一个有序列里,运用简单查找挨个挨个找,那么需要猜测的次数与列表长度是相同的,这也被称为线性时间。
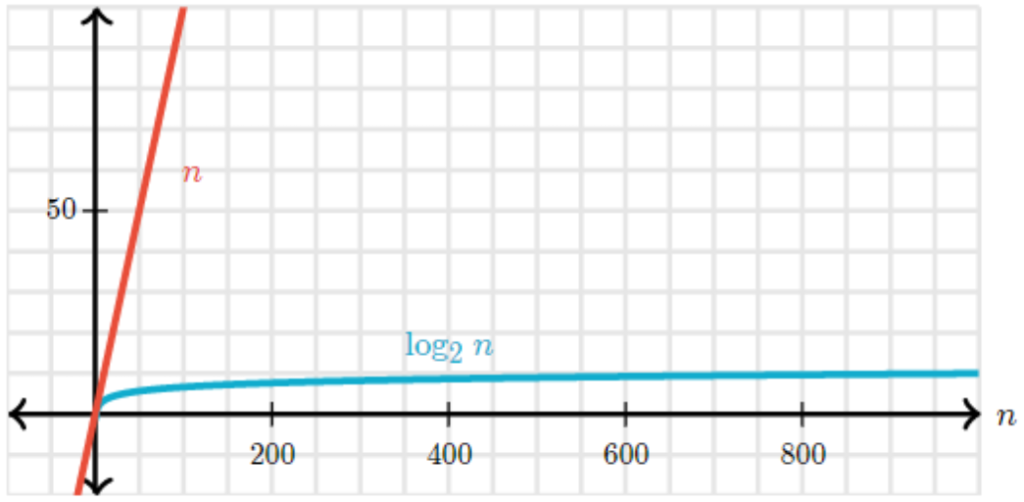
二分查找,假设一种好的情况——每次都取一半区间。如果寻找的目标值所在列表包含100个元素,那最多猜7次。假设为40亿个元素,那最多只需猜测32次!这种情况被称为对数时间。要知道,对数函数的y随着x的增大而增大的速率是越来越小的。所以,二分查找的时间复杂度可以表示为O(logN)。
代码如何实现二分法
想象一下玩猜数字的过程吧,在1到100猜我此时此刻内心想着的数字。你说的X值猜大了,我会把1到100提示到1到X;如果你说的X值猜小了,我会提示到X到100。继续…你终于猜到了,范围缩减到就一个数,即你猜的这个值。
用代码实现以上步骤,思考我需要什么变量,需要哪些流程逻辑代码:
- left = 0,right = 100
- 你猜的值也需要一个变量保存
- 比较,缩小范围,直到你猜到我所想
使用while循环实现
arr是猜测的数组,x是要寻找的值。
//while循环写法
let whileFunction = function (arr, x) {
let start=0, //数组第一个值的下标
end=arr.length-1; //数组最后一个值的下标
// 只要范围没有缩小到只包含一个元素
while (start<=end){
// 同时要考虑内存溢出的问题
let mid=Math.floor(start + (end - start)/2);
if (arr[mid]===x) return true;
// 判断x在左边还是右边
else if (arr[mid] < x) {
start = mid + 1;
} else {
end = mid - 1;
}
}
return false; //找不到
}
使用递归实现
可以用while循环实现,那就可以转成递归。
let binarySearchFunction = function (arr, x, start, end) {
// 也就相当于不满足while(left<=right)
if (start > end) return false;
// 同时要考虑内存溢出的问题
let mid=Math.floor(start + (end - start)/2);
// 和目标值x对比,一次命中
if (arr[mid]===x) return true;
//如果你猜的中间值大于目标值
if(arr[mid] > x) {
return binarySearchFunction(arr, x, start, mid-1);
}//end -> mid - 1;
else {
return binarySearchFunction(arr, x, mid+1, end);
}//start -> mid + 1;
}
使用二分法解决问题
上面的代码的条件,可以看到,我们循环判断的条件是start<= end,或者终止条件是start>end。为什么呢?
因为我们二分的时候,要走了包含目标值的那一半边。那最后我们得到目标值,也就是得到只含一个目标值的数组,所以是start=end=目标值在数组的位置下标。
但是,有时候我们已经得到最后一个只包含一个元素的数组了,但是他不等于目标值X!!没关系,在start==end的情况下,继续执行start = mid + 1,或者end = mid – 1~那下一次肯定就退出循环了。
以上都是说要找目标值的问题,那要是找不到,我想把这个要找的目标值插入进数组呢?该怎么解决?上一道题看看。
探索插入位置
题目导航?:搜索插入位置

其实我想说,我们在搜索之前,并不知道是不是有这个数值,有就返回下标呗。没有就暂且返回null,再去慢慢思考如何正确返回这个数值应该插入的位置。(真的,在我看来,学习算法真的是一种陶冶情操的过程,不要急,不要求做题有多厉害,不要求模板套得6不6)
思考到的点有如下:
- 这题是要返回数组下标的,所以end和start的取值和之前一样是没有毛病的!
- 每次结束顺换的情况是,start>end 。在(start=end=mid)的最后一次循环里,要不就是因为我们要插入的数组小于最终剩下的那个值而end=mid-1,此时要插入的值应插入到最终剩下的那个值得左边,也就是要替代这个值的位置(坐标为left的值),后面的元素全部往后移;要不就是大于最终剩下的那个值而start=mid+1,此时要插入的值应插入到最终剩下的那个值的右边(也就是要在这个值的后边位置(坐标加一也就是mid+1);
发现没有发现没有发现没有(激动地搓手跳跃~)!他最终要插入的位置下标,就等于循环结束后的left值!
有一种情况,要是数值小于第一个数或者大于最后一个数呢?那这个想法还管用吗?
我想说,管用!可以试想,我要是插入数值最后,那我是不是意味着大于原先数组的最后一个数值,那left = mid + 1,不就是原先数组的最后一个元素的下标加一吗?
所以这是我对于这道题的解法:
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var searchInsert = function(nums, target) {
let low = 0,
high = nums.length - 1,
while(low <= high) {
const mid = parseInt((low+high)/2);
let guess = nums[mid];
if (guess == target) {
return mid;
} if (guess < target ) {
low = mid+1;
} else {
high = mid-1;
}
}
return low; //这是唯一的变动,也是题目所要求的返回目标值该插入的位置下标
};
总结
这就是二分法。我也是边写边总结的,所以写起来肯定也有不足之处。有时候做二分题出错,我也是在纸上一遍遍画我代码逻辑的运行过程,慢慢总结。如果您有更好的想法或者可以指出我的不足之处,非常欢迎联系~